[ИУ9] Основы информатики

Домашнее задание №3

Реализуйте процедуру derivative, находящую производную функции одной переменной по правилам дифференцирования. Пусть процедура принимает один аргумент — выражение на языке Scheme, которой задана функция, и возвращает также выражение на языке Scheme, соответствующее производной. Выражения должны быть пригодны для выполнения с помощью встроенной процедуры eval.

Реализуйте нахождение производных константы, линейной, степенной, показательной (включая экспоненту), натурального логарифма, тригонометрических функций (синуса и косинуса), а также суммы, произведения, частного и композиции функций. Не следует ограничивать число слагаемых в сумме, множителей в произведении и функций в композиции. Упрощение выражений не требуется.

Ваша процедура должна находить решения по крайней мере следующих примеров:

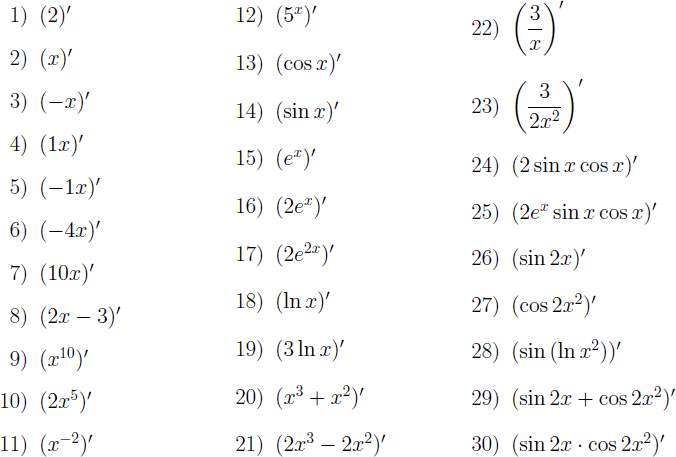
Примеры

Примеры вызова процедуры:

(derivative '(expt x 10)) ⇒ (* 10 (expt x 9))
(derivative '(* 2 (expt x 5))) ⇒ (* 2 (* 5 (expt x 4)))
(derivative (list '* 'x 'x)) ⇒ (+ (* x 1) (* 1 x))

Рекомендации:

  1. Выбирайте наиболее общие формулы дифференцирования, обработку частных случаев разрабатывайте только при необходимости.

  2. Так как упрощение выражений не предусматривается, вполне приемлемым будет результат вычисления, например, вида (* 3 (/ 1 x)), или (* 2 (expt x 1)), или (* 0 (* 2 (expt x 2))).

  3. Разрабатывайте программу через тестирование. Для этого реализуйте каркас для юнит-тестирования. На основе приведенных выше примеров напишите набор тестов для вашей процедуры и ведите разработку так, чтобы добиться правильного выполнения всех тестов. Выполняйте тесты после каждого внесения изменений и дополнений в вашу программу.

  4. Предложите способ сделать тесты нечувствительными к способу представления результата, где это возможно. Например, (* (exp x) (sin x)) на (* (sin x) (exp x))) и (/ 3 x) (* 3 (/ 1 x)) должны проходить один и тот же тест.

«Ачивки»