[ИУ9] Основы информатики
Лекция 13. Основы лексического и синтаксического анализа
Формальная грамматика — это способ описания синтаксиса языков программирования.
Мы будем рассматривать не все языки программирования, а только контекстно-свободные и регулярные (автоматные).
Формальная грамматика — набор правил, позволяющих породить строку, принадлежащую данному языку программирования. Формальная грамматика состоит из
- аксиомы,
- множества терминальных символов,
- множества нетерминальных символов и
- множества правил грамматики.
Терминальные символы — символы алфавита, из которых строятся строки данного языка программирования. Для стадии лексического анализа (грамматики токенов) терминальные символы — литеры (characters) текста. Для стадии синтаксического анализа терминальные символы — токены.
Нетерминальные символы — символы, которые раскрываются согласно правилам грамматики.
В синтаксическом дереве (дереве разбора) терминальные символы соответствуют листьям, нетерминальные — внутренним узлам.
Аксиома грамматики — нетерминальный символ, выбранный в качестве стартового.
Правила грамматики описывают, как в строке символов (терминальных и нетерминальных) раскрываются нетерминальные символы.
Порождение строки, принадлжежащей языку, начинается с аксиомы, заканчивается цепочкой терминальных символов.
Контекстно-свободные языки — языки, правила грамматик которых описываются выражением вида
X → a b c …
где X — нетерминальный символ, a, b, c — некоторые символы грамматики.
При описании грамматик для наглядности пустую строку обозначают знаком ε.
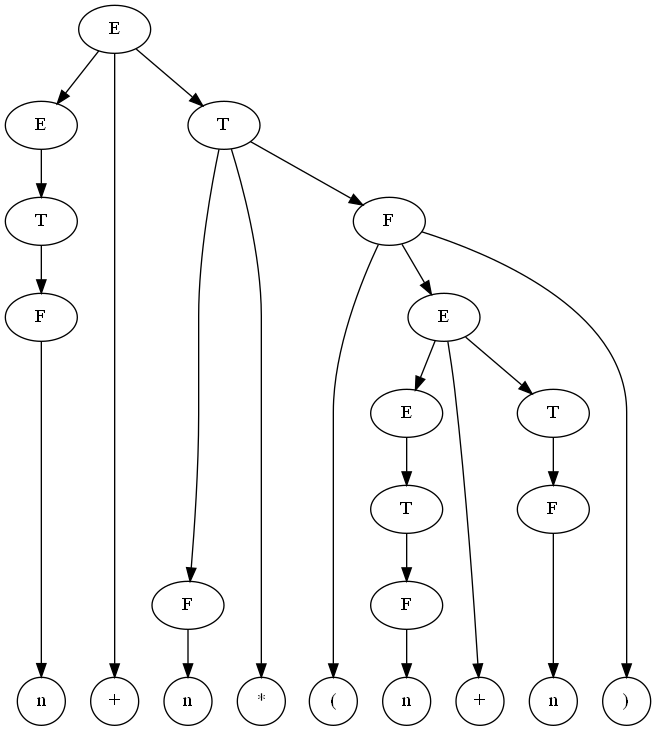
Грамматика арифметических выражений:
- аксиома
E, - терминальные символы:
+,*,n(некоторое число),(,). - нетерминальные символы:
E,T,F. - правила
E → T E → E + T T → F T → T * F F → n F → (E)
Часто правила с общими левыми частями (нетерминалами) объединяют, разделяя варианты
знаком |.
E → T | E + T
T → F | T * F
F → n | ( E )
Пример вывода в этой грамматике:
E → E + T → E + T * F → T + T * F → F + T * F →
↑ ↑ ↑ ↑ ↑
→ n + T * F → n + T * (E) → n + F * (E) → n + n * (E) →
↑ ↑ ↑ ↑
→ n + n * (E + T) → n + n * (T + T) → n + n * (F + T) →
↑ ↑ ↑
→ n + n * (n + T) → n + n * (n + F) → n + n * (n + n)
↑ ↑
Дерево вывода для этого примера:
Задача синтаксического анализа — имеем цепочку нетерминальных символов, нужно построить дерево разбора, соответствующее этой цепочке или показать, что такового не существует — цепочка не принадлежит данному языку. Т.е. для некоторой грамматики и некоторой строки определить, принадлежит ли данная строка языку, описываемому данной грамматикой.
Способы описания грамматики
Форма Бекуса-Наура (БНФ) — способ описания грамматики, где правила имеют вид
<Нетерминал> ::= альтернатива | … | альтернатива
нетерминалы записываются в угловых скобках (<…>), терминальные символы
записываются или сами собой (для знаков операций, например), или словами
БОЛЬШИМИ БУКВАМИ. Альтернативные варианты разделяются знаками |.
Пример:
<Выражение> ::= <Слагаемое> | <Выражение> + <Слагаемое>
<Слагаемое> ::= <Множитель> | <Слагаемое> * <Множитель>
<Множитель> ::= ЧИСЛО | ( <Выражение> )
Впервые она была использована при описании Алгола-60.
При описании многих языков программирования (в учебниках, стандартах) используется
тот или иной вариант БНФ. Нотация может быть расширена такими обзначениями как
* или + после нетерминала, означающие повторение ноль или более раз (*)
или один или более раз (+) данного нетерминала.
Как правило, если записана грамматика языка программирования, то под аксиомой
подразумевается самый первый нетерминал (в примере <Выражение>).
Синтаксические диаграммы — это графический способ описания грамматики языка. Впервые был использован Никлаусом Виртом при описании синтаксиса языка Паскаль в 1973 году.
Используются редко, т.к. грамматика в виде БНФ более компактная и её проще записывать (диаграммы нужно рисовать).
LL(1)-грамматики
LL(k)-грамматики — грамматики, в которых мы можем определить правило для
раскрытия нетерминала по первым k символам входной цепочки.
Дано: цепочка терминальных символов и нетерминальный символ. Требуется определить, по какому правилу нужно раскрыть нетерминальный символ, чтобы получить префикс этой цепочки. Для LL(k)-грамматик это можно сделать, зная первые k символов.
Чаще всего рассматриваются LL(1)-грамматики, где раскрытие определяется по первому символу.
Пример: не-LL(k)-грамматика:
E → T | E + T
T → F | T * F
F → n | ( E )
Если имеем строку n * n * n + n + n и нетерминал E, то мы не знаем, по какому
правилу нужно раскрывать E. Поскольку в начале строки может быть сколько
угодно сомножителей, в общем случае, чтобы выбрать правило раскрытия для E
(т.е. E → T или E → E + T), нужно прочитать неизвестное количество входных
знаков. А для LL(k)-грамматики k должно быть конечно и фиксировано.
Пример: LL(1)-грамматика для тех же арифметических выражений:
E → T E′
E′ → ε | + T E′
T → F T′
T′ → ε | * F T′
F → n | ( E )
здесь ε — пустая строка. В данной грамматике мы всегда можем определить
применимое правило. Например, для E правило только одно, его используем.
Для E′: если строка начинается на +, то выбираем вторую ветку E′ → + T E′,
иначе выбираем первую E′ → ε. Для F: знак n выбирает первую ветку, знак
( — вторую.
Пример не-LL(1)-грамматики:
A → B x z
B → ε | x y
Для строки x … и нетерминала B мы не можем определить раскрытие по первому
символу, т.к. допустимо и то, и другое правило. Язык включает в себя две строки:
x z и x y x z. По первому символу невозможно определить правило для B.
Однако, это грамматика LL(2). По первым двум символам определить раскрытие можно.
Также грамматика не LL(1) если разные правила начинаются с одинаковых символов:
A → x a | x b
Грамматика не LL(1), если в правилах имеем т.н. левую рекурсию:
A → x | A y
Преимущество LL(1)-грамматик — для них сравнительно легко написать синтаксический анализатор методом рекурсивного спуска.
Метод рекурсивного спуска
Метод рекурсивного спуска — способ написания синтаксических анализаторов для LL(1)-грамматик на алгоритмических языках программирования. Для каждого нетерминала грамматики записывается процедура, тело которой выводится из правил для данного нетерминала.
Построенный синтаксический анализатор выдаёт сообщение о принадлежности входной строки к заданному языку.
Написание синтаксического анализатора состоит из этапов:
- Составление LL(1)-грамматики для данного языка программирования.
- Формальное выведение парсера из правил грамматики. Парсер либо молча принимает строку, либо выводит сообщение об ошибке.
- Наполнение парсера семантическими действиями — построение дерева разбора, выполнение проверок на корректность типов операций, возможно даже, вычисление результата в процессе разбора.
Вспомогательная структура данных — поток (stream).
У потока есть возможность получить текущий символ (peek stream) без продвижения
вперёд, получить символ и удалить из потока (next stream).
Пример реализации потока: stream.scm.
Все функции, соответствующие нетерминалам, принимают поток, первым символом которого должен быть первый символ раскрытия нетерминала, и функцию ошибки, которая вызывается, чтобы прервать разбор. При успешном разборе функция поглощает из входного потока все токены, соответствующие раскрытию данного нетерминала.
(define (nterm stream error)
…)
Пусть w — некоторая строка символов грамматики (терминальных и нетерминальных).
Обозначим FIRST(w) — множество терминальных символов, с которого может начинаться
строка токенов, полученная из w раскрытием всех нетерминалов. Если строка может
быть пустой, то ε также входит в FIRST(w).
Построим множество FIRST(w) для правил грамматики арифметических выражений:
E → T E′
E′ → ε | + T E′
T → F T′
T′ → ε | * F T′
F → n | ( E )
FIRST(E) = FIRST(T) = FIRST(F) = { n, ( }
FIRST(E′) = { +, ε }
FIRST(+ T E′) = { + }
FIRST(* F T′) = { * }
FIRST(T′) = { *, ε }
…
Пусть правило имеет вид
nterm → alt1 | … | altN
Если среди альтернатив есть такая altK, что ε ∈ FIRST[altK], то она должна
быть последней.
Функция для нетерминала имеет вид, если FIRST[altN] не содержит ε:
(define (nterm stream error)
(cond (( (peek stream) ∈ FIRST[alt1] ) PARSE[alt1] )
…
(( (peek stream) ∈ FIRST[altK] ) PARSE[altK] )
…
(( (peek stream) ∈ FIRST[altN] ) PARSE[altN] )
(else (error #f))))
Если FIRST[altN] содержит ε, то функция имеет вид
(define (nterm stream error)
(cond (( (peek stream) ∈ FIRST[alt1] ) PARSE[alt1] )
…
(( (peek stream) ∈ FIRST[altK] ) PARSE[altK] )
…
(( (peek stream) ∈ FIRST[altN−1] ) PARSE[altN−1] )
(else PARSE[altN])))
Функция PARSE[w] описывает последовательность команд для разбора
правой части правила w:
PARSE[] → #t
PARSE[term w] → (expect stream term error) PARSE[w]
PARSE[nterm w] → (nterm stream error) PARSE[w]
где функция (expect stream term error) имеет вид
(define (expect stream term error)
(if (equal? (peek stream) term)
(next stream)
(error #f)))
Разбор начинается с создания потока и сохранения точки возврата. После успешного разбора аксиомы в потоке должен располагаться символ конца потока.
(define (parse tokens)
;; Создаём поток
(define stream (make-stream tokens))
;; Создаём точку возврата
(call-with-current-continuation
(lambda (error)
;; разбираем аксиому
(axiom stream error)
;; в конце должен остаться признак конца потока
(equal? (peek stream) #f))))
Практические советы:
- В конец списка символов, которые потребляет лексический анализатор, в конец списка токенов, которые потребляет синтаксический анализатор, нужно обязательно добавлять признак конца ввода (EOF, end-of-file).
- На практике язык разделяют на два «слоя»: лексику и синтаксис. Лексика языка определяет набор «слов», лексем, на которые бьётся программа, по лексемам создаются токены, которые группируются в синтаксическое дерево. Смысл в том, что раздельное описание лексики и синтаксиса гораздо проще, чем писать грамматику для всего сразу.
- Удобно определить тип «поток», как описано выше.
- Для прерывания разбора при ошибке рекомендуется использовать продолжение.
Лексический анализ
Грамматика для стадии лексического анализа описывается, как правило, без рекурсии (имеется ввиду, без нехвостовой рекурсии), т.к. лексическая структура языка не требует вложенных конструкций.
Назначение лексического анализа: разбивает исходный текст на последовательность токенов, которые синтаксический анализ будет группировать в дерево. Либо, если исходный текст не соответствует грамматике — выдача сообщения (сообщений) об ошибке.
Входные данные: строка символов (или список символов), выходные:
последовательность токенов. Можно сказать, что дерево разбора для грамматики
лексем вырожденное — рекурсия есть только по правой ветке (cdr).
Мы будем его реализовывать методом рекурсивного спуска.
Синтаксический анализ
Его грамматика как правило описывается уже с использованием рекурсии, дерево разбора рекурсивное.
Назначение: построение синтаксического дерева из списка токенов. Либо выдача сообщения об ошибке.
Входные данные: список токенов, выходные: дерево разбора (или синтаксическое дерево).
Дерево разбора — дерево, построенное для данной грамматики и данной входной строки, такое что, корнем является аксиома грамматики, листьями — символы входной строки, внутренними узлами являются нетерминальные символы грамматики, потомки внутренних узлов упорядочены и соответствуют правилам грамматики, при перечислении листьев слева-направо получаем исходную строку.

Абстрактное синтаксическое дерево отражает уже логическую, смысловую структуру программы. В отличие от дерева разбора, оно не содержит скобок для указания приоритета, символов-разделителей и т.д.
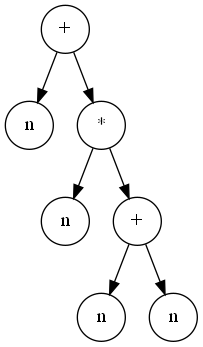
Для построения абстрактного синтаксического дерева функцию PARSE[w] можно
модифицировать следующим образом:
PARSE[s1 s2 ... sN] →
(let* ((sym1 PARSE-SYM[s1])
(sym2 PARSE-SYM[s2])
...
(symN PARSE-SYM[sN]))
‹построение узла дерева из sym1…symN›)
PARSE-SYM[term] → (expect stream term error)
PARSE-SYM[nterm] → (nterm stream error)
Разумеется, в реальной программе переменным sym1 … symN нужно давать
осмысленные имена.
Пример лексического и синтаксического анализа
В качестве примера рассмотрим подмножество Scheme с переменными, лямбдами, определениями и вызовами функций.
Первая фаза написание парсера — построение LL(1)-грамматики.
(load "stream.scm")
; Подмножество языка Scheme
; <sequence> ::= <term> <sequence> | <empty>
; <empty> ::=
; <term> ::= <define> | <expr>
; <define> ::= (DEFINE VAR <expr>)
; <expr> ::= VAR | <lambda> | <call>
; <lambda> ::= (LAMBDA <varlist> <sequence>)
; <call> ::= (<expr> <exprs>)
; <exprs> ::= <empty> | <expr> <exprs>
;
; Лексика:
; <tokens> ::= <token> <tokens>
; | <spaces> <tokens>
; | <empty>
; <spaces> ::= SPACE <spaces> | <empty>
; <token> ::= "DEFINE" | "LAMBDA" | "(" | ")" | <variable>
; <variable> ::= LETTER | <variable> LETTER | <variable> DIGIT
Проблема этой грамматики, что она не LL(1).
Грамматика, приведённая к LL(1):
; <sequence> ::= <term> <sequence> | <empty>
; <empty> ::=
; <term> ::= <define> | <expr>
; <define> ::= (DEFINE VAR <expr>)
; <expr> ::= VAR | (<complex-const>)
; <complex-constr> ::= <lambda> | <call>
; <lambda> ::= LAMBDA <varlist> <sequence>
; <call> ::= <expr> <exprs>
; <exprs> ::= <empty> | <expr> <exprs>
;
; Лексика:
; <tokens> ::= <token> <tokens>
; | <spaces> <tokens>
; | <empty>
; <spaces> ::= SPACE <spaces> | <empty>
; <token> ::= "(" | ")" | <variable-or-keyword>
; <variable-or-keyword> ::= LETTER <variable-tail>
; <variable-tail> ::= <empty>
; | LETTER <variable-tail>
; | DIGIT <variable-tail>
Вторая фаза — механистическое построение парсера по грамматике. Построим лексический анализатор:
(define (scan str)
(define stream
(make-stream (string->list str) (integer->char 0)))
(call-with-current-continuation
(lambda (error)
(tokens stream error)))
(equal? (peek stream) (integer->char 0)))
; <tokens> ::= <spaces> <tokens>
; | <token> <tokens>
; | <empty>
(define (tokens stream error)
(define (start-token? char)
(or (char-letter? char)
(char-digit? char)
(equal? char #\()
(equal? char #\))))
(cond ((char-whitespace? (peek stream))
(spaces stream error)
(tokens stream error))
((start-token? (peek stream))
(token stream error)
(tokens stream error))
(else #t)))
; <spaces> ::= SPACE <spaces> | <empty>
(define (spaces stream error)
(cond ((char-whitespace? (peek stream))
;(if (char-whitespace? (peek stream))
; (next stream)
; (error #f))
(next stream))
(else #t)))
(define char-letter? char-alphabetic?)
(define char-digit? char-numeric?)
; <token> ::= "(" | ")" | <variable-or-keyword>
(define (token stream error)
(cond ((equal? (peek stream) #\() (next stream))
((equal? (peek stream) #\)) (next stream))
((char-letter? (peek stream))
(variable-or-keyword stream error))
(else (error #f))))
; <variable-or-keyword> ::= LETTER <variable-tail>
(define (variable-or-keyword stream error)
(cond ((char-letter? (peek stream))
;(if (char-letter? (peek stream))
; (next stream)
; (error #f))
(next stream)
(variable-tail stream error))
(else (error #f))))
; <variable-tail> ::= LETTER <variable-tail>
; | DIGIT <variable-tail>
; | <empty>
(define (variable-tail stream error)
(cond ((char-letter? (peek stream))
(next stream)
(variable-tail stream error))
((char-digit? (peek stream))
(next stream)
(variable-tail stream error))
(else #t)))
Третья фаза — реализация семантических действий. В случае лексического анализа — это построение цепочки токенов.
(define (scan str)
(let* ((EOF (integer->char 0))
(stream (make-stream (string->list str) EOF)))
(call-with-current-continuation
(lambda (error)
(define result (tokens stream error))
(and (equal? (peek stream) EOF)
result)))))
; <tokens> ::= <spaces> <tokens>
; | <token> <tokens>
; | <empty>
;
; (tokens stream error) -> list of tokens
(define (tokens stream error)
(define (start-token? char)
(or (char-letter? char)
(char-digit? char)
(equal? char #\()
(equal? char #\))))
(cond ((char-whitespace? (peek stream))
(spaces stream error)
(tokens stream error))
((start-token? (peek stream))
(cons (token stream error)
(tokens stream error)))
(else '())))
; <spaces> ::= SPACE <spaces> | <empty>
;
; (spaces stream error) -> <void>
(define (spaces stream error)
(cond ((char-whitespace? (peek stream))
;(if (char-whitespace? (peek stream))
; (next stream)
; (error #f))
(next stream))
(else #t)))
(define char-letter? char-alphabetic?)
(define char-digit? char-numeric?)
; <token> ::= "(" | ")" | <variable-or-keyword>
;
; (token stream error) -> token
(define (token stream error)
(cond ((equal? (peek stream) #\() (next stream))
((equal? (peek stream) #\)) (next stream))
((char-letter? (peek stream))
(variable-or-keyword stream error))
(else (error #f))))
; <variable-or-keyword> ::= LETTER <variable-tail>
;
; (variable-or-keyword stream error) -> SYMBOL
(define (variable-or-keyword stream error)
(cond ((char-letter? (peek stream))
;(if (char-letter? (peek stream))
; (next stream)
; (error #f))
(string->symbol
(list->string (cons (next stream)
(variable-tail stream error)))))
(else (error #f))))
; <variable-tail> ::= LETTER <variable-tail>
; | DIGIT <variable-tail>
; | <empty>
;
; (variable-tail stream error) -> List of CHARs
(define (variable-tail stream error)
(cond ((char-letter? (peek stream))
(cons (next stream)
(variable-tail stream error)))
((char-digit? (peek stream))
(cons (next stream)
(variable-tail stream error)))
(else '())))